公差分析与分配计算表下载:https://www.cad2d3d.com/dl.php?ID=1142
1.0 术语定义
1.1 标准偏差 σ
标准偏差(Std Dev,Standard Deviation) 统计学名词。一种度量数据分布的分散程度之标准,用以衡量数据值偏离算术平均值的程度。标准偏差越小,这些值偏离平均值就越少,反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。标准偏差是方差的算术平方根。
标准差也被称为标准偏差,标准差(Standard Deviation)描述各数据偏离平均数的距离(离均差)的平均数,它是离差平方和平均后的方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度,标准偏差越小,这些值偏离平均值就越少,反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。平均数相同的两个数据集,标准差未必相同。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。这两组的平均数都是70,但A组的标准差应该是17.078分,B组的标准差应该是2.160分,说明A组学生之间的差距要比B组学生之间的差距大得多。
总体标准偏差与样本标准偏差区别:
总体标准偏差:针对总体数据的偏差,所以要平均, 取值1/N。
样本标准偏差,也称实验标准偏差:针对从总体抽样,利用样本来计算总体偏差,为了使算出的值与总体水平更接近,就必须将算出的标准偏差的值适度放大,取值1/(N-1)。

1.2 上限值UL和下限值LL
上限值(upper Limit),下限值(Lower Limit),上限值和下限值由设计决定。
1.3 过程能力指数
名词解释:
- Cp:Process Capability Index
- Cpk:adjusted for mean shift
- UL:零件规格上限
- LL:零件规格下限值
- u:规格中心值
- X:平均数
- T:公差规格=规格上限-规格下限
1.3.1 双侧规格
过程能力指数双侧规格计算公式:Cp=T/6σ=(UL-LL)/6σ
式中,T为过程统计量的技术规格的公差幅度;UL、LL分别为上、下公差界限;σ为过程统计量的总体标准差,可以在过程处于稳态时得到。
1.3.2. 有偏移情形
有偏移情形的过程能力指数:当过程统计量的分布均值X与公差中心u不重合(即有偏移)时,显然不合格率增大,也即Cp值降低,因此采用 Cp=T/6σ=(UL-LL)/6σ 所计算的过程能力指数不能反映有偏移的实际情形,需要加以修正。
Ca:过程准确度,反映平均值偏离中心值的程度。
Ca=(平均值-中心值)/规格公差的一半=(X-u)/0.5T
Cpk=Cp(1-Ca)
1.3.3 单侧规格
单侧规格情形的过程能力指数:若只有规格上限的要求,而对规格下限无要求,则过程能力指数计算如下:Cpu=(UL-X)/3σ,若只有规格下限的要求,而对规格上限无要求,则过程能力指数计算如下:Cpl=(X-LL)/3σ
1.3.4 Cpk计算实例

1.4 正态分布
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布,且其概率密度函数为:
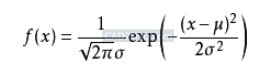
则这个随机变量X就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ,σ2); ,读作X服从N(μ,σ2),或X服从正态分布。
正态分布曲线关于μ对称,并在μ处取最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点,形状呈现中间高两边低,正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。
μ是正态分布的位置参数,描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大,而取离μ越远的值的概率越小。正态分布以X=μ为对称轴,左右完全对称。正态分布的期望、均数、中位数、众数相同,均等于μ。
正态分布图形特性:
- 集中性:正态曲线的高峰位于正中央,即均数所在的位置。
- 对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
- 均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
- 曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。
当μ=0,σ=1时,正态分布就成为标准正态分布,概率密度函数为:
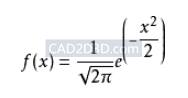
为了应用方便,常对正态分布变量X作变量变换,该变换(规范化值Z)使原来的正态分布转化为标准正态分布(standard normal distribution),Z被称为标准正态变量或标准正态离差(standard normal deviate)或规范化值。
Z=(X-mean)/standard_dev
实际工作中,常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数,以便估计该区间的例数占总例数的百分数(频数分布)或观察值落在该区间的概率。正态曲线下一定区间的面积可以通过查表求得。对于正态或近似正态分布的资料,已知均数和标准差,就可对其频数分布作出概约估计。
1.5 均匀分布
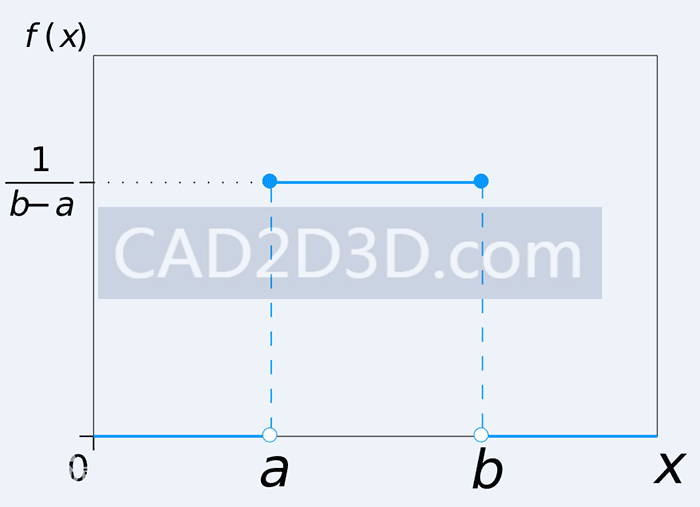
均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
在区间(a,b)上服从均匀分布的随机变量X,具有下述意义的等可能性,即它落在区间(a,b)中任意等长度的子区间内的可能性是相同的。或者说它落在(a,b)的子区间内的概率只依赖于子区间的长度而与子区间的位置无关。
均匀分布的概率密度函数为:
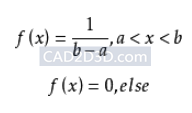
对于平均值μ和方差σ2,概率密度可以写为(疑问):
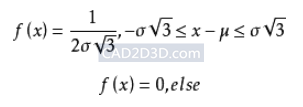
随机变量:U(a,b)
X的概率密度函数:f(x)=1/(b-a) a<x<b 其它x,f(x)=0;
X的平均值:E(X)=∫(b,a) xf(x)dx=∫(b,a)xdx/(b-a)=0.5x^2/(b-a)|(b-a)=(a+b)/2
X的方差:D(X)=Var(X)=∫(b,a)[x-E(X)]² dx/(b-a)=∫(b,a)[x-(a+b)/2]² dx/(b-a)=(b-a)²/12
2.0 公差分析表使用说明
2.1 含有四种公差分析方法:
- 极端最坏情形法
- 统计法RSS(Root Sum Squares)—使用3σ;尺寸数据呈正态或均匀分布
- 6西格玛 (6σ)—使用Cp和Cpk
- 测量数据法—使用零件的测量数据
自动生成带有上限额下限值的正态分布图。
自动计算超过上限值和下限值的不合格率,并且预估可接受的装配体合格率(百分比或百万分率)。
不需要蒙特卡罗模拟,只需输入每个尺寸的均值和3西格玛偏差。
标准Excel电子表格,不需要.dll文件,不需要宏功能。
2.2 复杂装配体
产品通常是由多个零件组装而成,因此组成装配体的各个零件的尺寸偏差经过累积叠加后,最终会影响装配体尺寸。
公差分析可以根据现有过程能力和设计要求,定量的分析装配体的累积误差,最终预测产品的合格率等。
2.3 过程变化
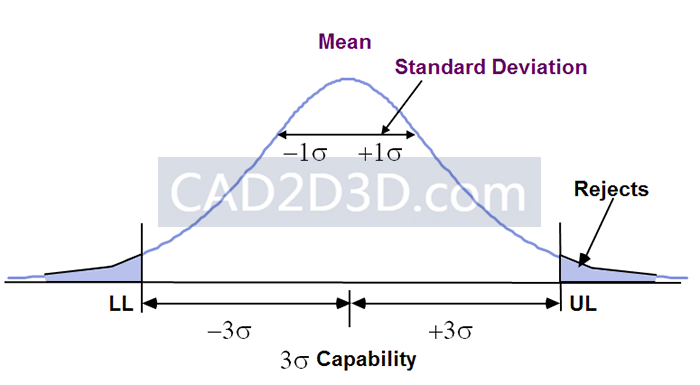
正态分布图
制造过程中,每个零件的尺寸都存在偏差,大多数零件的尺寸将聚集在平均值附近,这种分布状态就是正态分布(或高斯分布),分布的平均值标志着曲线上的最高点。
分布的扩散程度由其标准偏差表示。均值表示该过程与目标值的接近程度。标准偏差表示精度或过程能力。
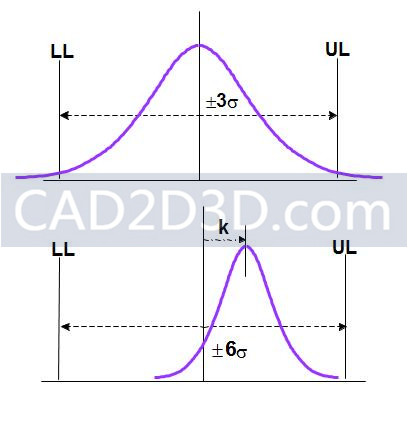
UL和LL标记尺寸的上限和下限,由设计要求设定。如果UL和LL对应于±3s处理能力,如图所示,将拒绝很少的部件(大约每1000个部件3个)。
2.4 装配体公差预测数学模型
公差分析的4种方法
- 极端最差情况法 Worst Case (WC)
- 统计法 Statistical (RSS)
- 6西格玛法 Six Sigma (6σ)
- 测量数据法 Measured Date
通过现有的零件尺寸数据,可以计算出零件尺寸的平均值和标准偏差,判断过程能力达到何种水平,在零件生产之前,通过公差分析,进一步完善对应零件的公差值(设计要求值)。
公差分析可以识别那个零件的尺寸对装配体尺寸影响最大,一般生产条件下,图纸标注的公差值对应 ±3σ的过程能力,即Ti=±3σ。
| 方法 | 公式 | 预测 | 应用场景 |
| Worst Case (WC) | 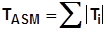 | 极端情况 无统计 | 关键系统 不能出现不合格品 成本最高 |
| Statistical (RSS) | 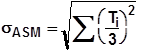 | 可能的偏差 部分不合格品 | 合理估计 允许部分不良品 成交较低 |
| Six Sigma (6σ) | 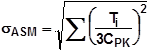 | 长期偏差 部分不合格品 | 随时间推移平均值会与中心值产生偏差 高品质水平要求 |
| Measured Data (Meas) | 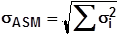 | 现有零件的偏差 部分不合格品 | 零件已生产 What-if? 研究 |
极端最差情况 Worst Case (WC):在极端最坏情况,组成装配体的所有零件的尺寸同时处于上限值或下限值,此时组成的装配体偏差为各零件偏差之和,并将此值作为装配体的尺寸要求,在此情况下,不会出现不良品,但势必会要求各个零件的偏差值很小,生产成本很高。
统计法 Statistical(RSS)(Root Sum Squares):将各个零件的偏差求平方和然后开方,可以预测不合格品率。
6西格玛法 Six Sigma (6σ):基于RSS,但零件的公差大于3σ,长期生产过程中均值会发生偏移,目标质量水平4.5σ。
测量数据法:是产品已生产,根据实际产品的测量数据来计算平均值、标准偏差、Cpk等。
2.5 平均值偏移
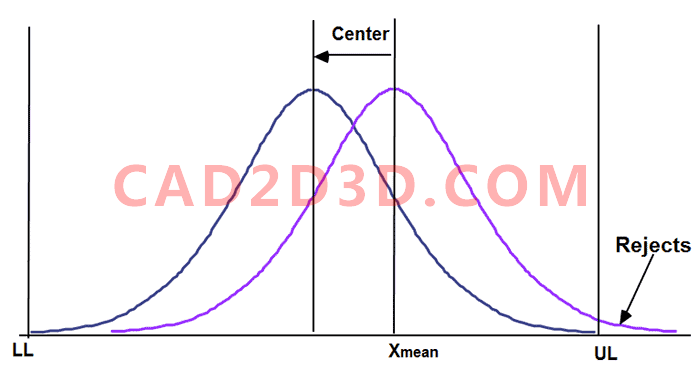
零件的实际尺寸的平均值通常都会偏离中心值(UL-LL)/2,平均值偏移会造成不合格率增高。
2.6 减少分布的标准偏差
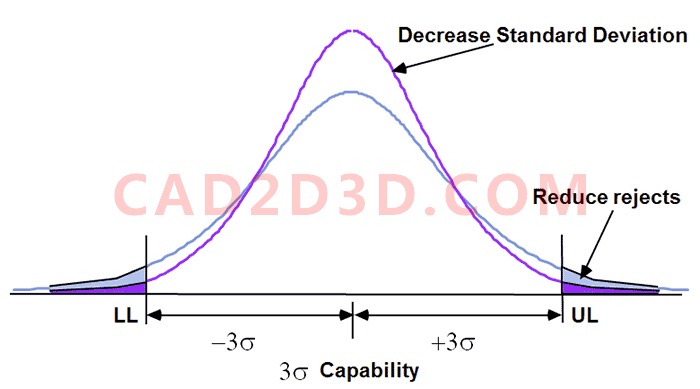
减小标准偏差可以降低不合格品率,为减少尺寸标准偏差,会对生产过程提出更高要求。
2.7 放宽尺寸上下限要求意味着更多的合格产品
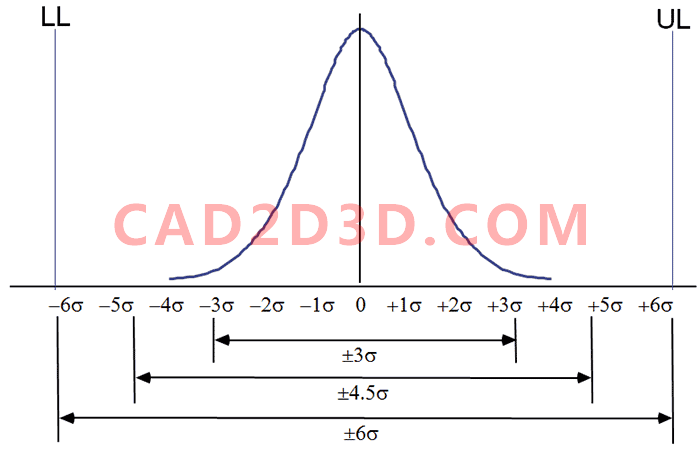
一般情况下,尺寸偏差对应3σ,若将尺寸偏差放宽至6σ,意味着更多的合格产品。
2.8 控制(减小)标准偏差 减少不合格品
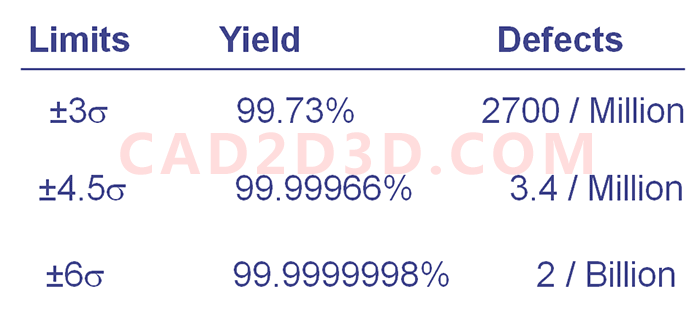
UL和LL不是任意选择的,它们是设计师根据设计要求设定的限制,根据分析和测试,将它们设置在一定水平,以确保最终产品的正常性能。没有工程师评估,UL和LL不能更改。
装配体公差分配给各个零件,然后通过执行公差分析来设置各个零件的尺寸公差,以确保所提出的零件公差在添加时不会超过指定的装配公差。
2.9 平均值偏移
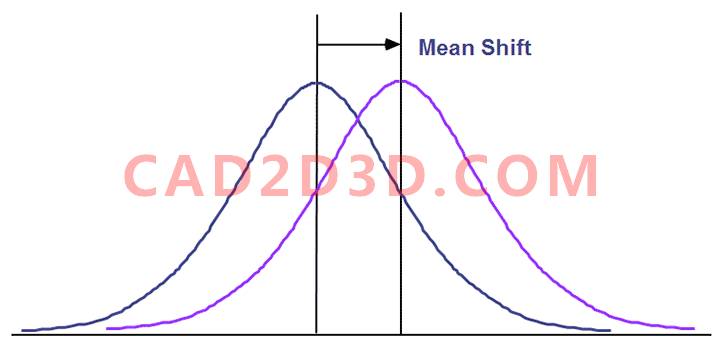
平均值会因为各种因素变化而发生偏移。
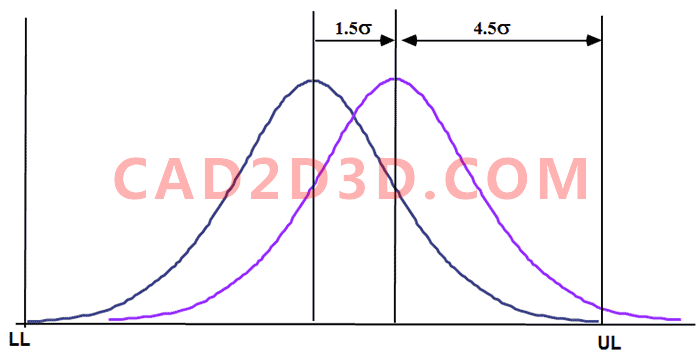
上图中UL和LL设置为±6σ,理想情况下平均值和中心值重合,整个分布呈正态分布,而实际运行时,平均值偏离中心值1.5σ,UL距离平均值为4.5σ,平均值左端没有不合格品,只有平均值右端会产生不合格品,不合格率相当于4.5σ水平的一半,因此约有1.7ppm不合格品出现,由于平均值偏移造成不合格率扩大至1000倍。
因此,为应对平均值1.5σ的偏移,并能保持4.5σ的质量水平,实际运行时需要保持6σ的过程质量。
这就是为什么许多大公司都在谈论6σ流程。他们实际上的目标是4到4.5秒的质量水平,但他们必须努力争取6σ附近的过程。
2.10 过程能力
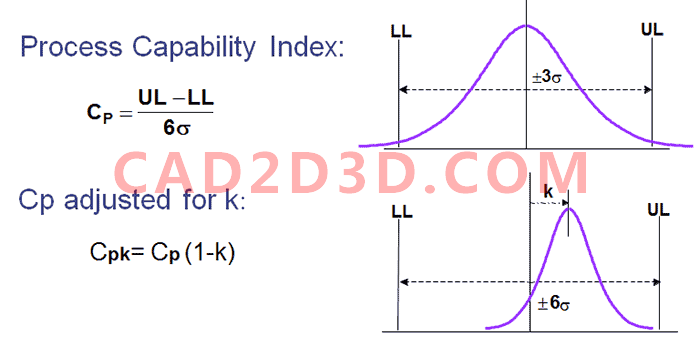
Cpk is just Cp multiplied by the factor (1-k), where k is a fraction between 0 and 1, If the mean has shifted 25% of the tolerance, that is, 0.25 of the distance from the mean to UL or LL, then Cp will be reduced by 75%. (此处有疑问,此处k请参见1.3.2)
2.11 6σ公差定义
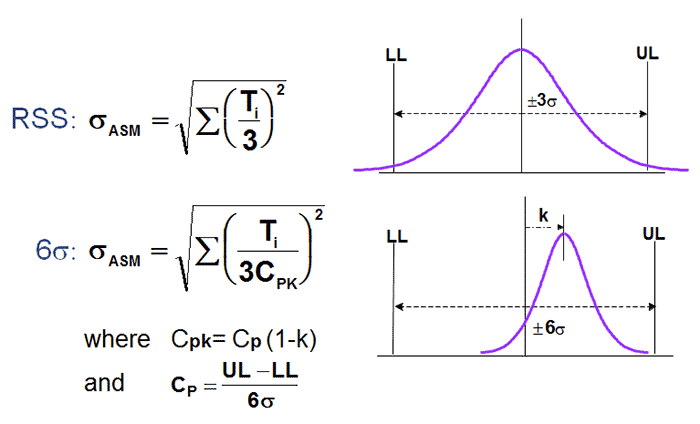
美国摩托罗拉公司最早提出“Six Sigma Program”,通过计算Cp和Cpk来评估过程能力。
零件的公差取值:Ti=3Cpiσi
当Cp=2时,要求零件的公差T为±6σ,也就是6σ水平时,Cp=2。
考虑到平均值偏移,零件的公差取值为:Ti=3Cpkiσi
2.12 6σ动态均值偏移
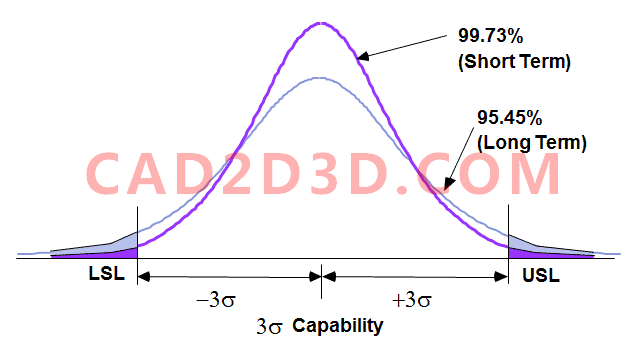
对于大批量生产,由于工具磨损,热膨胀,多腔模具等,均值可能会漂移,因此很难维持长时间的高水平过程制造能力。
摩托罗拉 Six Sigma 目标是维持长期的4.5σ质量水平,为了达到此水平,短期内必须达到6σ质量水平,即均值偏移量25%(k=0.25)
2.13 CATS 1-D 表格填写说明
CATS-1D 表格 颜色说明:蓝色字段用于用户输入,白色字段是中间计算,紫色代表自动生成的报告部分。
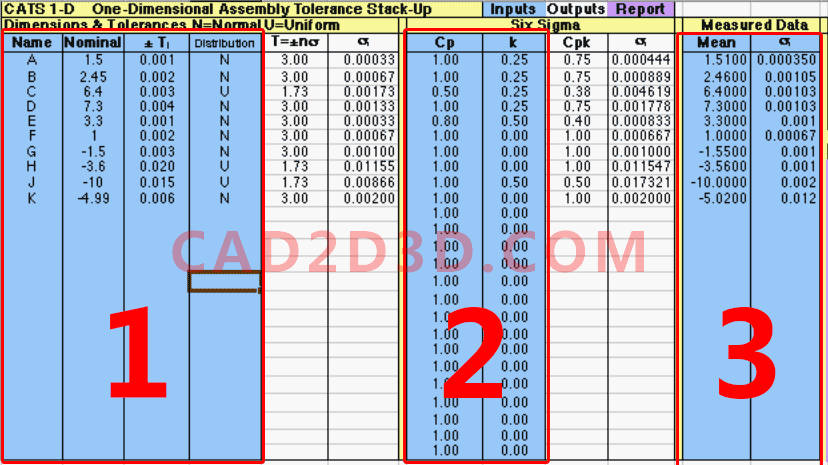
第一组蓝色列(设计数据):输入WC和RSS 基本尺寸和公差,这一列是设计要求。
Distribution(分布):此列为各个尺寸数据的分布情况,分为正态分布(Normal)和均匀分布(Uniform),通常尺寸数据都呈正态分布。
T=±nσ(公差):Distribution(分布)为正态分布式,n=3;Distribution(分布)为均匀分布时,n=√3(疑问);
Dimensions & Tolerances 栏中的 σi=Ti/n(n=3或n=√3)
第二组蓝色列(结合现有过程制造能力):输入Cp和k进行6σ分析,Cp、k、Cpk是现有的各个零件的实际过程能力,根据实际情况输入。
Six Sigma 栏中的 σi=Ti/(n*Cpk)
第三组蓝色列(成品数据):输入测量尺寸的平均值Mean和标准偏差σ,以及根据实际数据计算的标准偏差。
2.15 输出报告:4种公差分析方法计算出的各项值
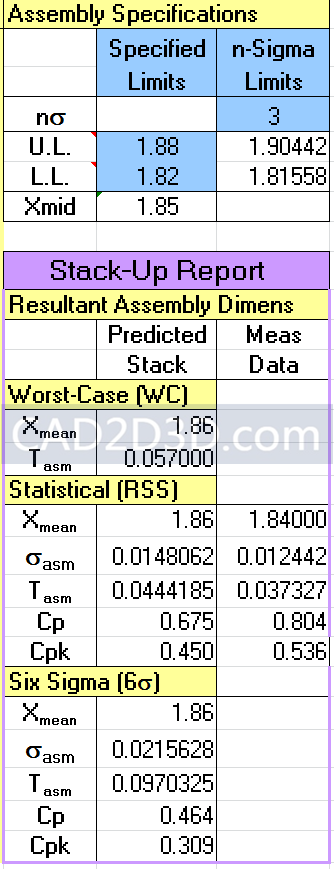
WC/RSS/Six Sigma 计算的值为预测值,Measured Data 计算的值为实际值。
RSS和Meas Date 在表格的相同行上,计算所采用的公式是相同的,只不过RSS输入的是设计值,而Meas Data 输入的是实际测量值。
RSS和Meas Data 中装配体公差Tasm=3σasm。
Six Sigma中装配体公差Tasm=4.5σasm(疑问 为何取4.5?)。
此表还有1个问题点:装配体规格值UL=1.88,LL=1.82,Xmid=1.85,而组成装配体的各项尺寸公称值相加后Xmean=1.86,Xmid和Xmean为什么不设计成一样的?
2.16 输出报告:合格率
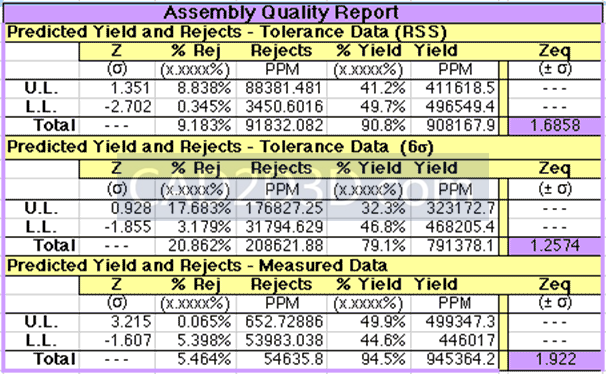
上表显示的是3种公差分析方法(RSS/6σ/Meas Date)预测的合格率。
上表中的Z列是正态分布的规范化值,Z=(X-mean)/standard_dev,X:需要的规范化值,mean:分布的算术平均值,standard_dev:分布的标准偏差。Excel表格中取规范化值的公式为 Z=STANDARDIZE(x, mean, standard_dev)。
上表中的 % Rej 列是不合格率,先根据平均值(mean)、标准偏差(standard_dev)求解规范化值(Z),然后根据规范化值求解累积分布函数(合格率)。
需要使用Excel表中的NORM.S.DIST(z,cumulative)函数,该函数可以返回累积分布函数(面积)。
NORM.S.DIST 函数参数说明:
Z:需要计算其分布的数值。
Cumulative:是一个决定函数形式的逻辑值。如果 Cumulative 为 TRUE,NORMS.DIST 返回累积分布函数;如果为 FALSE,则返回概率密度函数。





