泵的扬程表征离心泵所产生的动能,在泵性能曲线或泵特性曲线中会有扬程这个参数。pump head is used to measure the kinetic energy which a centrifugal pump creates. It can be shown in the figure as the performance curve or pump characteristic curve.
泵扬程和特性曲线 Pump Head – Performance Curve
在流体动力学中,泵扬程用于表征泵产生的动能。扬程是泵根据泵赋予液体的动能产生的不可压缩流体柱高度的测量值。扬程和流量决定了泵的性能,图中以图形方式表示为性能曲线或泵特性曲线。使用扬程而不是压力来确定离心泵性能的主要原因是,液柱的高度不取决于液体的比重(密度),而泵的压力会发生变化。就压力而言,泵扬程 (ΔPpump) 是系统背压与泵入口压力之间的差值。In fluids dynamics the term pump head is used to measure the kinetic energy which a pump creates. Head is a measurement of the height of the incompressible fluid column the pump could create from the kinetic energy, that the pump gives to the liquid. The head and flow rate determine the performance of a pump, which is graphically shown in the figure as the performance curve or pump characteristic curve. The main reason for using head instead of pressure to determine the performance of a centrifugal pump is that the height of the fluid column is not dependent on the specific gravity (weight) of the liquid, while the pressure from a pump will change. In terms of pressure the pump head (ΔPpump) is difference between system back pressure and the inlet pressure of the pump.
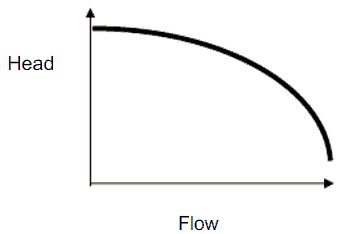
离心泵的最大扬程主要由泵叶轮的外径和轴角速度(旋转轴的速度)决定。扬程也会随着通过泵的体积流量的增加而变化。pump head - performace curve - chartThe maximum pump head of a centrifugal pump is mainly determined by the outside diameter of the pump’s impeller and the shaft angular velocity – speed of the rotating shaft. The head will also change as the volumetric flow rate through the pump is increased.
离心泵可以保持的泵扬程与体积流量 (Q) 之间的关系取决于泵的各种物理特性,例如:The relationship between the pump head and the volumetric flow rate (Q), that a centrifugal pump can maintain, is dependent on various physical characteristics of the pump as:
- 提供给泵的功率 the power supplied to the pump
- 泵轴的角速度 the angular velocity of shaft
- 叶轮类型和直径 the type and diameter of the impeller
以及流体特性 and the used fluid:
- 密度 fluid density
- 粘度 fluid viscosity
这种关系非常复杂,需要对离心泵进行广泛的水压测试才能分析扬程和流量之间的关系。从下图中可以看出。This relationship is very complicated and its analysis lies in extensive hydraulic testing of certain centrifugal pump. As can be seen from the picture below.
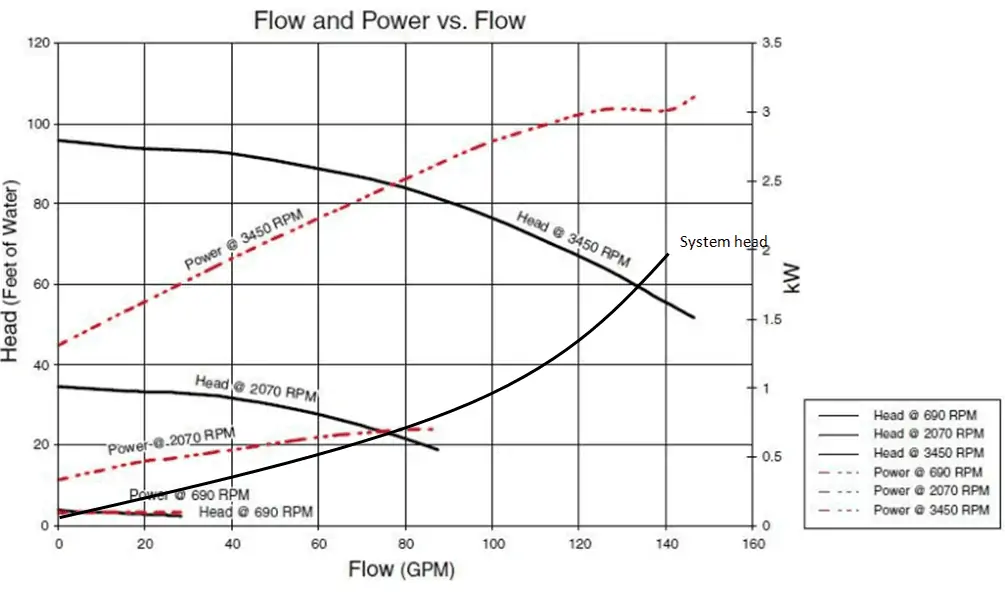
案例:泵性能计算 Example: Pump Performance Calculation
本例泵扬程计算,如何预估下列参数 Pump Head CalculationIn this example, we will see, how to predict:
- 设计流量 the design discharge
- 功率 water horsepower
- 扬程 the pump head
对于离心泵,根据 Euler’s turbomachine 方程可知 of a centrifugal pump. This performance data will be derived from the Euler’s turbomachine equation:
轴扭矩 Shaft torque:
Tshaft = ρQ(r2Vt2 – r1Vt1)
功率 Water horsepower:
Pw=ω.Tshaft = ρQ(u2Vt2 – u1Vt1)
泵扬程 Pump head:
H=Pw / ρgQ= (u2Vt2 – u1Vt1)/g
离心泵的参数如下Given are the following data for a centrifugal water pump:
叶轮内径和外径 diameters of the impeller at the inlet and outlet:
- r1 = 10 cm
- r2 = 20 cm
转速为1500转/分钟 Speed = 1500 rpm (revolutions per minute)
叶轮入口角度 the blade angle at inlet β1 = 30°
叶轮出口角度 the blade angle at outlet β2 = 20°
叶轮在入口和出口处的宽度 assume that the blade widths at inlet and outlet are:b1 = b2 = 4 cm.
求解过程 Solution:
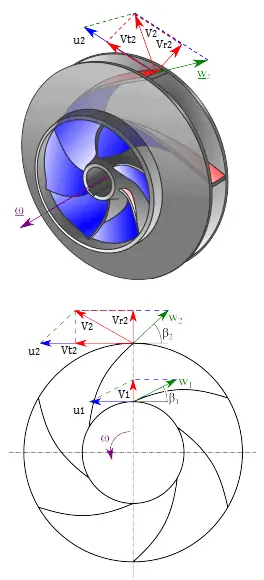
首先,我们必须计算出口处流动的径向速度。从速度图中,径向速度等于(我们假设流动正好垂直于叶轮进入,因此速度的切向分量为零)。First, we have to calculate the radial velocity of the flow at the outlet. From the velocity diagram the radial velocity is equal to (we assume that the flow enters exactly normal to the impeller, so tangential component of velocity is zero):
Vr1 = u1 tan 30° = ω r1 tan 30° = 2π x (1500/60) x 0.1 x tan 30° = 9.1 m/s
流速的径向分量决定了进入叶轮的体积流量。所以当我们知道 Vr1 在入口处时,我们可以根据以下方程确定该泵的排放量。这里 b1 表示入口处叶轮的叶片宽度。Radial component of flow velocity determines how much the volume flow rate is entering the impeller. So when we know Vr1 at inlet, we can determine the discharge of this pump according to following equation. Here b1 means the blade width of the impeller at inlet.
Q = 2π.r1.b1.Vr1 = 2π x 0.1 x 0.04 x 9.1 = 0.229 m3/s
为了计算所需的功率(Pw),我们必须确定出口切向流速 Vt2,因为已经假设入口切向速度 Vt1 等于零。In order to calculate the water horsepower (Pw) required, we have to determine the outlet tangential flow velocity Vt2, because it has been assumed that the inlet tangential velocity Vt1 is equal to zero.
出口径向流速由 Q 守恒得出 The outlet radial flow velocity follows from conservation of Q:
Q = 2π.r2.b2.Vr2 ⇒ Vr2 = Q / 2π.r2.b2 = 0.229 / (2π x 0.2 x 0.04) = 4.56 m/s
从图(速度三角形)出口叶片角度 β2 可以很容易地表示如下 From the figure (velocity triangle) outlet blade angle, β2, can be easily represented as follows。
cot β2 = (u2 – Vt2) / Vr2
因此出口切向流速 Vt2 为 and therefore the outlet tangential flow velocity Vt2 is:
Vt2 = u2 – Vr2 . cot 20° = ω r2 – Vr2 . cot 20° = 2π x 1500/60 x 0.2 – 4.56 x 2.75 = 31.4 – 12.5 = 18.9 m/s.
所需功率 The water horsepower required is then:
Pw= ρ Q u2 Vt2 = 1000 [kg/m³] x 0.229 [m³/s] x 31.4 [m/s] x 18.9 [m/s] = 135900 W = 135.6 kW
泵扬程为 and the pump head is:
H ≈ Pw / (ρ g Q) = 135900 / (1000 x 9.81 x 0.229) = 60.5 m
有很多朋友好象将“扬程”与“泵出口压力”搞混了。 扬程的定义将直观地说就是泵能将单位重量液体输送的高度,比如一台泵的扬程是50米,那么它打水时可以将水送到50米高处,打汽油(假设汽油密度为700kg/m3)时也只能将汽油送到50米高,打碱液(假设碱液密度为1200kg/m3)时也能将碱液送到50米高。 不同的是,如果打水时的功率需要10kw,那么打汽油时只需要7kw,而打碱液时则需要12kw。 还有出口压力也不同,如果打水时的出口压力是5公斤,那么打汽油时只有3.5公斤,而打碱液时则是6公斤。 所以,必须搞清“扬程”和“压力”的区别,扬程与介质密度 没有 关系。
扬程是泵固有的属性,跟介质密度没有关系。
参考文献:https://www.thermal-engineering.org/what-is-pump-head-performance-curve-of-centrifugal-pump-definition/
转载请注明:
文章作者: 尚延伟 原文链接:https://www.cad2d3d.com/post- 2062 .html
可能感兴趣的文章
 一橇多鹤管实物图,乙醇汽油装车鹤管
一橇多鹤管实物图,乙醇汽油装车鹤管 屋顶通风扇大全及实物图,通风扇中英文名称对照
屋顶通风扇大全及实物图,通风扇中英文名称对照 电子元器件图示,名称中英文对照,一图胜过千言万语
电子元器件图示,名称中英文对照,一图胜过千言万语- 压力管道行业仪表类相关产品手册、规格书和操作使用说明书等
 装车橇设计大师:闸阀、截止阀和止回阀
装车橇设计大师:闸阀、截止阀和止回阀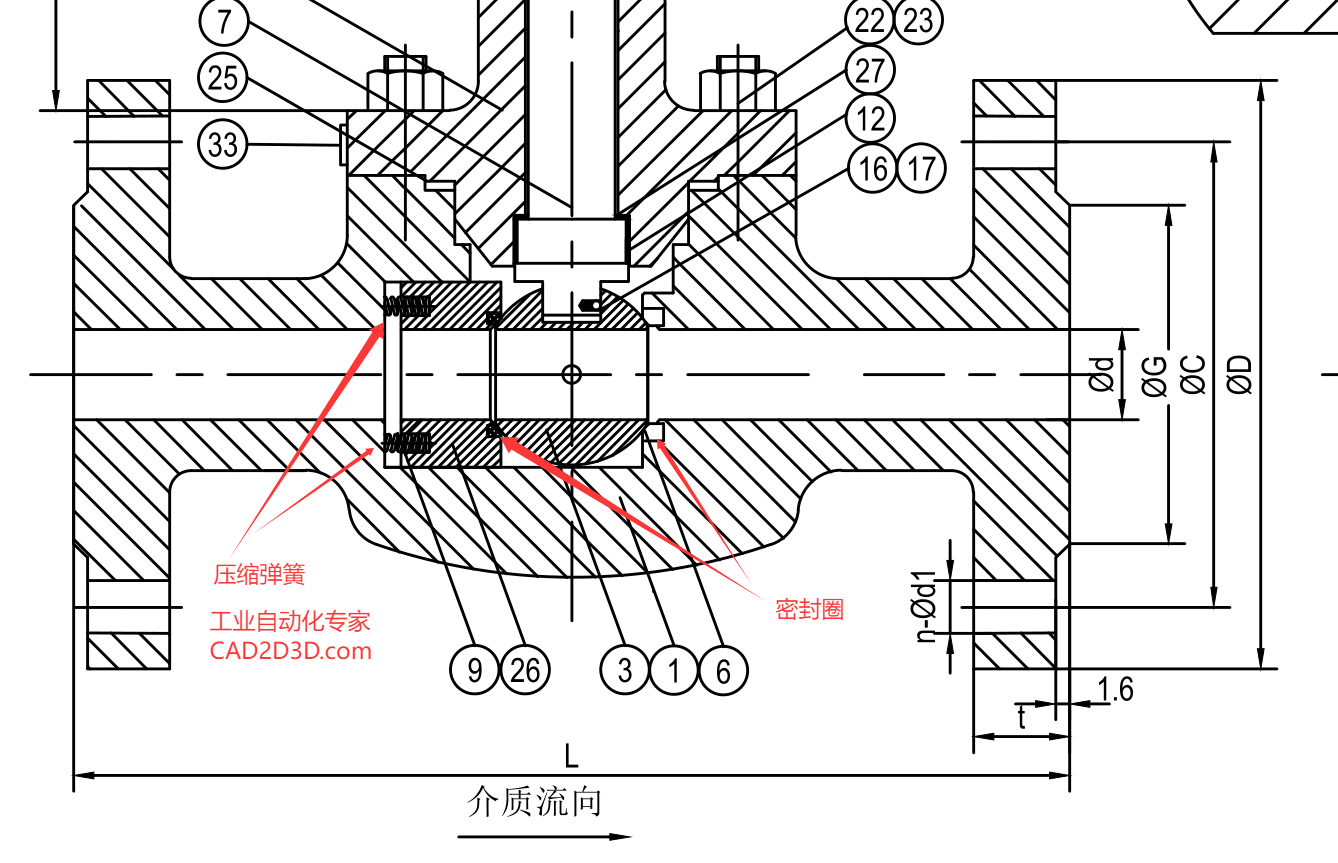 低温浮动球球阀阀座结构详解,含图纸及实物,浮动球单向密封有方向性
低温浮动球球阀阀座结构详解,含图纸及实物,浮动球单向密封有方向性- 球阀球体安装方式:顶装式TOP ENTRY、侧装式END ENTRY(Side Entry)和底装式BOTTOM ENTRY
 长见识了,去毛刺居然有这么多先进的方法,我还以为只能用刮刀和砂纸
长见识了,去毛刺居然有这么多先进的方法,我还以为只能用刮刀和砂纸- 德国博世力士乐 Bosch Rexroth 官网,全球领先的传动与控制技术供应商
 日本工匠手把手教你如何安装导轨滑块,高精度是靠装配来实现的
日本工匠手把手教你如何安装导轨滑块,高精度是靠装配来实现的
更多最新发布: 化工装备
-
GB 50093 自动化仪表工程施工及质量验收规范 温度、压力取源部件安装规定、条文解释说明及案例解析
-
电气装置应接地,螺栓应有防松装置,接线端子及紧固件应涂电力复合脂
-
 钢厂作业人员必备!饱和水蒸气球罐(球形蒸汽蓄热器)技术参数、生产制造过程、实物图及潜在失效模式分析
钢厂作业人员必备!饱和水蒸气球罐(球形蒸汽蓄热器)技术参数、生产制造过程、实物图及潜在失效模式分析
-
 绝了!LNG 工厂的终极神器竟然是自行车,电器全封杀,机械的含金量还在上升
绝了!LNG 工厂的终极神器竟然是自行车,电器全封杀,机械的含金量还在上升
-
 LPG、丙烷、丁烷等装卸车用 STANAG 3756 干式分离阀(干式快速接头)厂家品牌及产品介绍
LPG、丙烷、丁烷等装卸车用 STANAG 3756 干式分离阀(干式快速接头)厂家品牌及产品介绍
-
 LNG 罐箱(罐式集装箱) P&ID、阀门清单、3D效果图、实物图和装卸方法
LNG 罐箱(罐式集装箱) P&ID、阀门清单、3D效果图、实物图和装卸方法
-
 API 610 离心泵的泵型 OH1 和 OH2 的区别、图示及对应的实物图
API 610 离心泵的泵型 OH1 和 OH2 的区别、图示及对应的实物图
-
![你家燃气耐烧吗?燃气表入口压力对计量结果影响巨大,极端情况下计量结果相差2倍, [勘误:绝对压力波动很小,对体积影响很小,对计量结果的影响可以忽略不计]](https://www.cad2d3d.com/uploads/202601/ranqibiao.jpg) 你家燃气耐烧吗?燃气表入口压力对计量结果影响巨大,极端情况下计量结果相差2倍, [勘误:绝对压力波动很小,对体积影响很小,对计量结果的影响可以忽略不计]
你家燃气耐烧吗?燃气表入口压力对计量结果影响巨大,极端情况下计量结果相差2倍, [勘误:绝对压力波动很小,对体积影响很小,对计量结果的影响可以忽略不计]

 1.4万套solidworks非标自动化设备3D图纸机械设计SW建模三维模型
1.4万套solidworks非标自动化设备3D图纸机械设计SW建模三维模型  SolidWorks代画机械设计sw出图creo代做cad制图纸夹具ug建模代做
SolidWorks代画机械设计sw出图creo代做cad制图纸夹具ug建模代做  赠视频 机械制图与识图从入门到精通 图解机械工制图图样识读与绘制方法基础使用技巧实操案例解读 机械设
赠视频 机械制图与识图从入门到精通 图解机械工制图图样识读与绘制方法基础使用技巧实操案例解读 机械设 




 本站所有资源一键获取,含3D模型、设计软件和案例视频等
本站所有资源一键获取,含3D模型、设计软件和案例视频等 支付宝现金红包,又疯狂“大面积”送钱了!人均 1-20 元 (无套路/每天能领)
支付宝现金红包,又疯狂“大面积”送钱了!人均 1-20 元 (无套路/每天能领) AutoCAD 2025 破解版+注册机 安装程序免费下载,附下载地址及安装教程
AutoCAD 2025 破解版+注册机 安装程序免费下载,附下载地址及安装教程 SolidWorks 2024 SP2.0 破解版免费下载及安装教程
SolidWorks 2024 SP2.0 破解版免费下载及安装教程 发那科机器人 FANUC 离线编程 动画仿真模拟软件 ROBOGUIDE V9 免费下载
发那科机器人 FANUC 离线编程 动画仿真模拟软件 ROBOGUIDE V9 免费下载